主页 > 新闻 > 公司新闻

新闻

新闻资讯

联系我们

联系人：陈先生

手机：13888889999

电话：020-88888888

邮箱：youweb@126.com

地址：广东省广州市番禺经济开发区

公司新闻

在神经网络中weight decay起到的做用是什么？momentum呢？normalization呢？

作者：佚名发布时间：2024-03-11 12:16:27

weight decay是提高最终收敛的正确率的还是提高收敛速度的？
同理，momentum呢？normalization呢？

一、weight decay（权值衰减）的使用既不是为了提高你所说的收敛精确度也不是为了提高收敛速度，其最终目的是防止过拟合。在损失函数中，weight decay是放在正则项（regularization）前面的一个系数，正则项一般指示模型的复杂度，所以weight decay的作用是调节模型复杂度对损失函数的影响，若weight decay很大，则复杂的模型损失函数的值也就大。

二、momentum是梯度下降法中一种常用的加速技术。对于一般的SGD，其表达式为 $x \\leftarrow x-\\alpha \\ast dx$ , $x$ 沿负梯度方向下降。而带momentum项的SGD则写生如下形式：

$v=\\beta \\ast v -a\\ast dx\\\\$

$x \\leftarrow x+v$

其中 $\\beta$ 即momentum系数，通俗的理解上面式子就是，如果上一次的momentum（即 $v$ ）与这一次的负梯度方向是相同的，那这次下降的幅度就会加大，所以这样做能够达到加速收敛的过程。

三、normalization。如果我没有理解错的话，题主的意思应该是batch normalization吧。batch normalization的是指在神经网络中激活函数的前面，将 $wx+b$ 按照特征进行normalization，这样做的好处有三点：

1、提高梯度在网络中的流动。Normalization能够使特征全部缩放到[0,1]，这样在反向传播时候的梯度都是在1左右，避免了梯度消失现象。

2、提升学习速率。归一化后的数据能够快速的达到收敛。

3、减少模型训练对初始化的依赖。

单说momentum，我觉得上面几位的说法（momentum可以克服local minima和critical point）值得商榷。

最简单的梯度下降法是

$x_{t+1}=x_t -\\alpha \ abla f(x_t)$ .

对于ill-conditioned问题，梯度下降法中每次迭代的方向 $\ abla f(x_t)$ 都很接近于Hessian矩阵最小特征向量的垂直方向，对目标函数的改进很小。为此加入一个历史信息项

$d_{t+1}=\\beta d_t - \ abla f(x_t), \\beta >0$

$x_{t+1}=x_t + \\alpha d_{t+1}.$

这里的 $d_t$ 就称为动量项，作用是通过历史搜索方向的积累，消除相继搜索方向中相反的方向，而一致的方向则相互累加。

对动量项的分析，有两个方面。

第一，动量项是共轭梯度法的近似 Steepest descent with momentum for quadratic functions is a version of the conjugate gradient method。共轭梯度法使用以前的搜索信息来修正当前的梯度方向，使得搜索方向之间相互共轭

$d_k=\\beta_k d_{k-1}- g_k$ ,
其中 $\\beta_k={ g_k ^T g_k \\over g_{k-1}^Tg_{k-1}}$ 是共轭参数。共轭方向如下图，图片来自 Efficient BackProp， Efficient BackProp

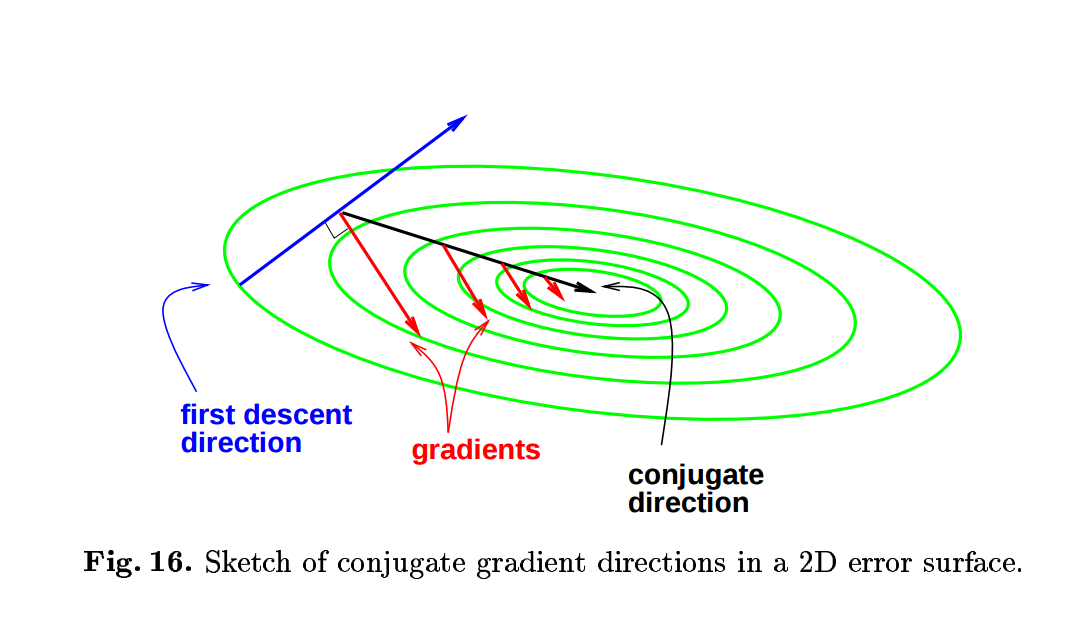
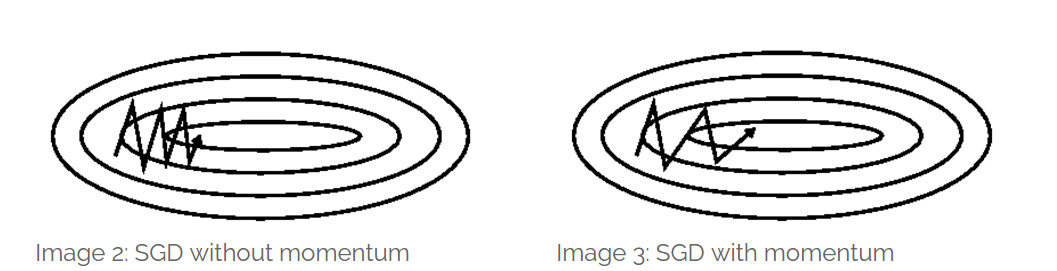
使用常数的 $\\beta$ 值，这就是momentum方法。换句话说，momentum 实际是共轭梯度法的近似。Momentum的作用也和共轭梯度法的作用相似，即通过使用历史搜索方法对当前梯度方向的修正来抵消在ill-conditioned 问题上的来回震荡。下图来自 An overview of gradient descent optimization algorithms

第二，使用动量项的优化方法是Newton方程/Hamilton 方程的离散化 On the momentum term in gradient descent learning algorithms。梯度下降法是梯度流

$\\frac{dx}{dt}=-\\epsilon \ abla f(x)$

的离散化，即

$\\frac{x_{t+\\delta t}- x_t}{\\delta t}=-\\epsilon \ abla f(x_t)$

$x_{t+\\delta t}=x_t -\\epsilon\\cdot \\delta t \ abla f(x_t)$ .

而含有动量项的优化方法，相当于将方程

$m\\frac{d^2x}{dt^2}+\\mu\\frac{dx}{dt}=- \ abla f(x)$

进行离散化。这是势能为 $f(x)$ 保守力场中，质量为m的质点在摩擦系数为 $\\mu$ 的介质中的运动方程。对此方程的二阶近似分析指出，带有momentum的时候，可以使用更大的学习率 $\\alpha$ 。

从这些分析出发，momentum主要是提高收敛速率的，并没有什么证据证明momentum对 local minima 比gradient descent 更加有效。Momentum term允许使用更大的学习率这一点对 critical point 可能有正面效果，不过具体的分析没有见到。在按点附近momentum的行为可见An overview of gradient descent optimization algorithms 最下面的动态图，其效果似乎值得怀疑。如果有人看到相关分析，请提醒我一下。

有哪些学术界都搞错了，忽然间有人发现问题所在的事情？ - 知乎用户的回答 - 知乎

启发式优化算法中，如何使之避免陷入局部最优解？ - 知乎用户的回答 - 知乎

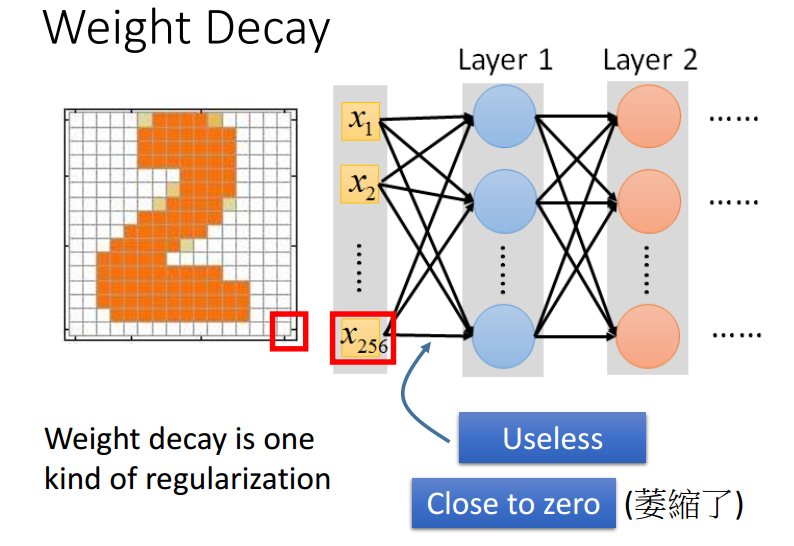
引用李宏毅的三张ppt

说说我对Weight Decay超参的理解。

在设置上，Weight Decay是一个L2 penalty，是对参数取值平方和的惩罚。

然而我们有大量的论文去考察参数的取值，发现

1. 不是高斯分布。

2. 取值可以量子化，即存在大量可压缩空间

3. 因为Relu, BN的存在使得其有界。

那么根据Loss function的设置求导之后，我们得到一个公式：

W( t+ 1)=W ( t ) ? lr ? delta(W)? lr ? wd ? W ( t )

也就是说，实际上我们可以把它化简为W(t)首先以（1- lr ? wd ）的比例等比例收缩，然后再根据学习率、梯度方向进行一次调整。

这个一收缩不要紧，我们现在做CNN已经不用Sigmoid+AveragePooling了，我们用的是Relu+MaxPooling，也就是说这一收缩，可能有的干脆就从激发变成了不激发。可有可无的激发也就消失掉了，有点像DropOut，当然如果这个Neuron真有用也可以回头再靠梯度把它学成激发状态。所以说有了这个东西会规避过拟合。

现在很少有流行模型使用DropOut了吧？窃以为，道理就在这。

最后，假设W只能取0和1两个值，那么L1-Penalty和L2-Penalty其实是等价的。实际上的W取值，是处于我说的这种极端情况和高斯分布之间的，所以按找传统统计里L2-Penalty的思路去思考Weight Decay是不对的。现在CNN里面有很多paper在滥用高斯假设，慎读。

========================================

补记：我通过对浅层宽模型设置2-3倍默认的Weight Decay往往效果是最好的。太大了实际会严重干扰第一个Learning Rate阶段的精度。太小了（也就是很多论文的默认设置）会距离收敛最优情形有差距。CIFAR100 Top-1 84.36%是在Weight Decay=0.001上获得的。也就是说，在实践里我比其他人更喜欢加大Weight Decay。

Weight decay 就是在进行梯度下降时用一个 $\\gamma$ 值（介于 0 到 1 之间）乘以当前计算中的每一个weight 。这么一来倒有几分 L2 regularization 的意思。

举个炒鸡简单的栗子。

f(a):=12n∑ $f(a):=\\frac{1}{2n}\\sum_{i=0}^{n}{(y_{i}?ax_{i})^{2}}$

其中，a 就是我们要优化的参数。

梯度下降走一波～～

$a_{m+1}=a_{m}- \\beta\\frac{1}{2n}\\sum_{i=0}^{n}({-2x_{i}(y_{i}- a_{m}x_{i})})=a_{m}+ \\beta\\frac{1}{n}\\sum_{i=0}^{n}{x_{i}(y_{i}- a_{m}x_{i})}=a_{m}+ \\beta*A - a_{m}\\beta*B$